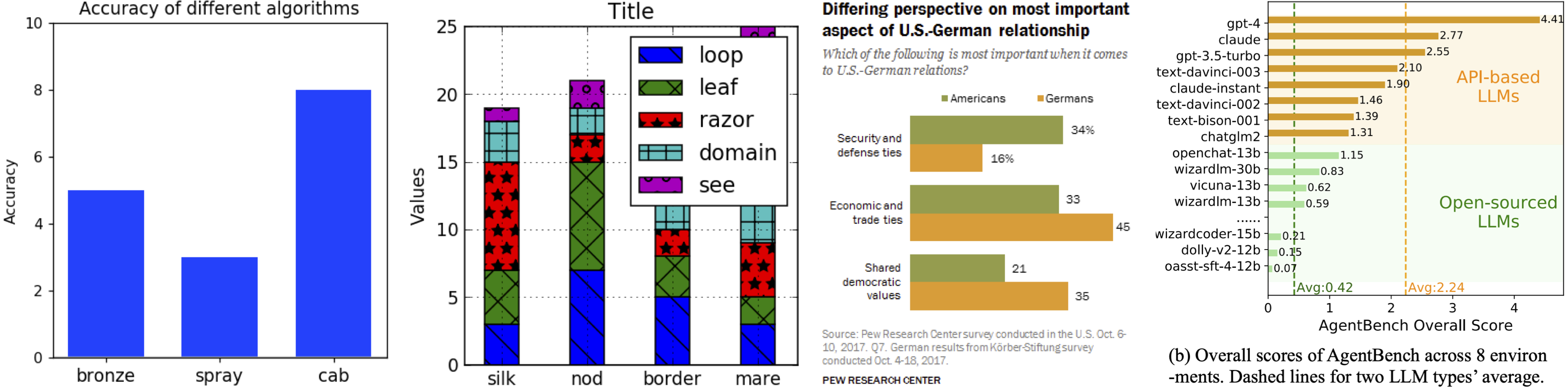
Accuracy scores on the testmini subset (1,000 examples) of 
MathVista.
MathVista
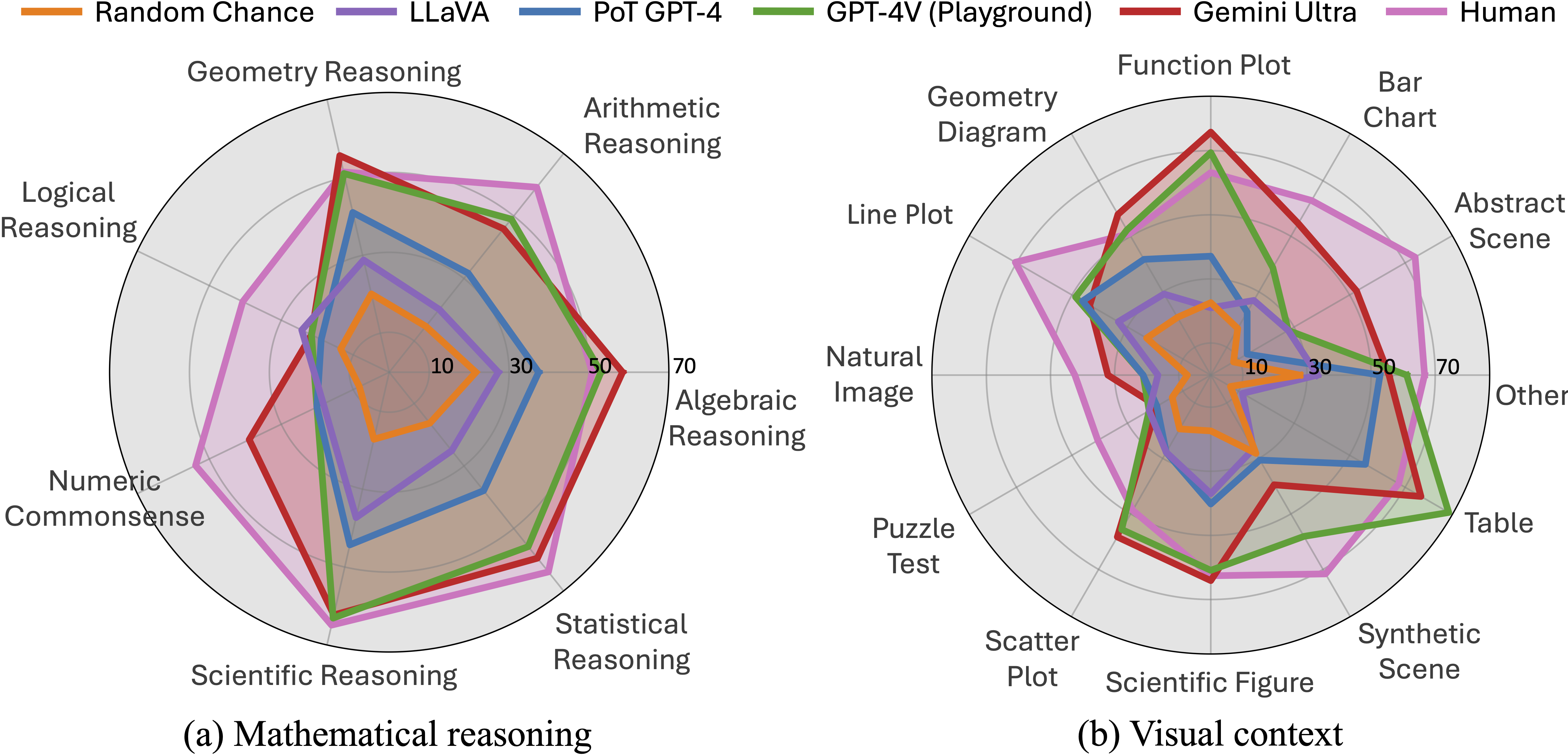
Accuracy scores of one leading LLM (i.e., PoT GPT-4), four primary LMMs, random chance, and human performance our proposed
MathVista
across mathematical reasoning and visual context types. PoT refers to program-of-thought prompting, and PoT GPT-4 is a textual LLM augmented with the caption and OCR text. GPT-4V is manually evaluated via the playground chatbot. The scores of Gemini Ultra are from the Gemini Team, Google.
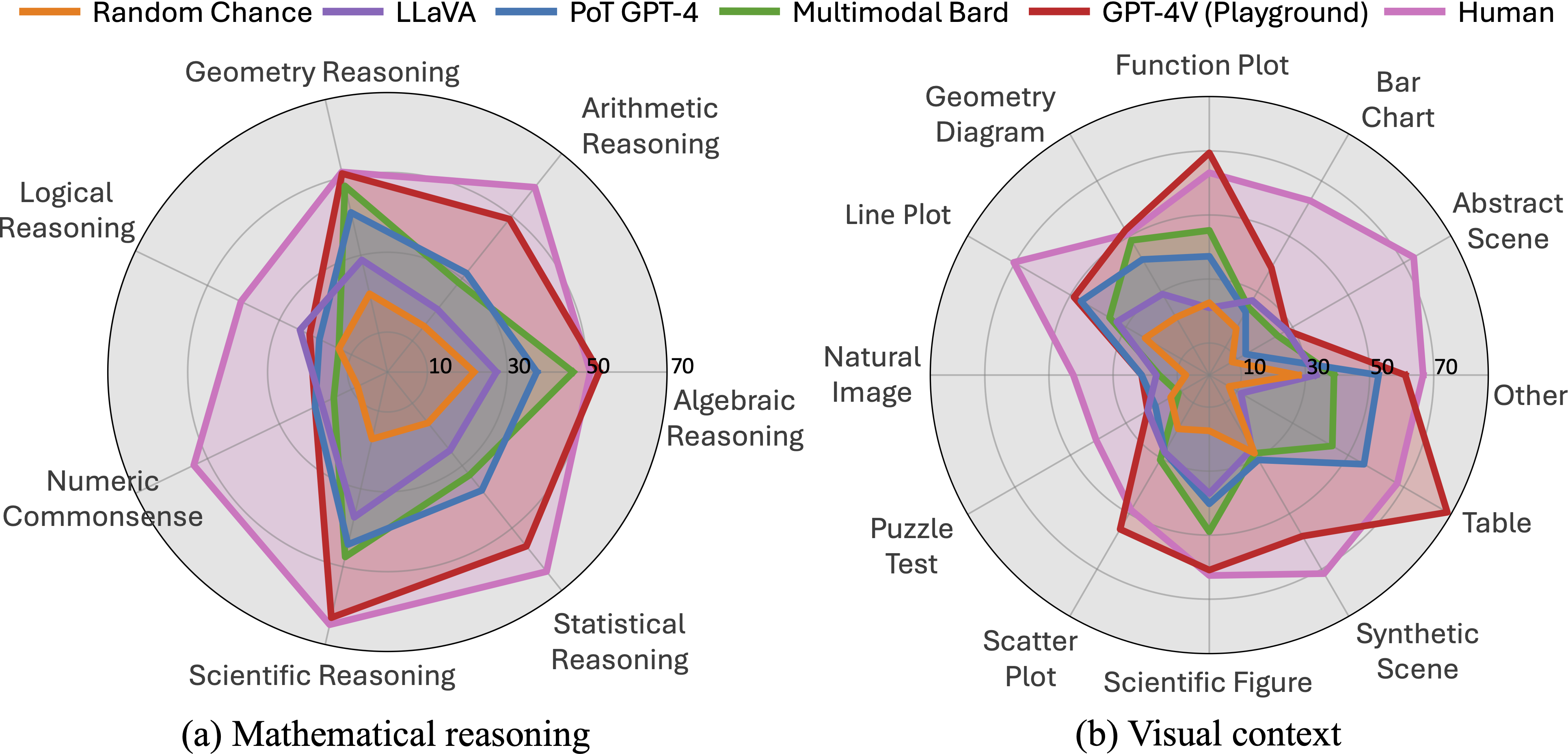
Accuracy scores of one leading LLM (i.e., PoT GPT-4), four primary LMMs, random chance, and human performance our proposed
MathVista
across mathematical reasoning and visual context types. PoT refers to program-of-thought prompting, and PoT GPT-4 is a textual LLM augmented with the caption and OCR text. GPT-4V is manually evaluated via the playground chatbot.
Large Language Models (LLMs) and Large Multimodal Models (LMMs) exhibit impressive problem-solving skills in many tasks and domains, but their ability in mathematical reasoning in visual contexts has not been systematically studied.
To bridge this gap, we present
MathVista, a benchmark designed to combine challenges from diverse mathematical and visual tasks. It consists of 6,141 examples, derived from 28 existing multimodal datasets involving mathematics and 3 newly created datasets (i.e., IQTest, FunctionQA, and PaperQA). Completing these tasks requires fine-grained, deep visual understanding and compositional reasoning, which all state-of-the-art foundation models find challenging.
With
MathVista, we have conducted a comprehensive, quantitative evaluation of 12 prominent foundation models. The best-performing GPT-4V model achieves an overall accuracy of 49.9%, substantially outperforming Bard, the second-best performer, by 15.1%. Our in-depth analysis reveals that the superiority of GPT-4V is mainly attributed to its enhanced visual perception and mathematical reasoning. However, GPT-4V still falls short of human performance by 10.4%, as it often struggles to understand complex figures and perform rigorous reasoning. This significant gap underscores the critical role that
MathVista will play in the development of general-purpose AI agents capable of tackling mathematically intensive and visually rich real-world tasks. We further explore the new ability of self-verification, the use of self-consistency, and the goal-directed multi-turn human-AI dialogues, highlighting the promising potential of GPT-4V for future research.
Accuracy scores on the testmini subset (1,000 examples) of
MathVista.
Accuracy scores on the test subset (5,141 examples with private ground truth) of
MathVista.
| # | Model | Method | Source | Date | ALL | FQA | GPS | MWP | TQA | VQA | ALG | ARI | GEO | LOG | NUM | SCI | STA |
| 1 | InternVL2-Pro 🥇 | LMM 🖼️ | Link | 2024-09-04 | 65.84 | 65.0 | 64.0 | 75.4 | 72.4 | 52.3 | 67.4 | 63.1 | 65.0 | 30.4 | 44.5 | 67.0 | 72.5 |
| 2 | InternVL2-8B-MPO 🥈 | LMM 🖼️ | Link | 2024-11-14 | 65.65 | 67.4 | 68.0 | 73.0 | 65.3 | 51.5 | 66.7/td> | 60.6 | 68.5 | 19.1 | 43.1 | 64.9 | 77.1 | 3 | InternVL-Chat-V1.2-Plus 🥉 | LMM 🖼️ | Link | 2024-02-22 | 60.18 | 52.2 | 56.2 | 78.3 | 61.6 | 55.5 | 56.0 | 64.4 | 57.6 | 21.6 | 46.1 | 60.0 | 60.1 |
| 4 | InternLM-XComposer2-VL-7B | LMM 🖼️ | Link | 2024-01-22 | 57.93 | 53.9 | 56.4 | 77.1 | 58.4 | 43.2 | 54.8 | 57.6 | 58.0 | 16.5 | 47.6 | 59.1 | 62.5 |
| 5 | Qwen-VL-Plus | LMM 🖼️ | Link | 2023-12-26 | 44.33 | 55.9 | 34.7 | 29.7 | 58.8 | 42.4 | 40.7 | 35.4 | 36.6 | 21.6 | 30.4 | 55.9 | 56.3 |
| 6 | SPHINX-MoE | MoE 🤖 | Link | 2024-01-13 | 42.68 | 50.3 | 29.7 | 40.9 | 49.3 | 43.3 | 33.9 | 43.0 | 29.1 | 14.4 | 26.3 | 46.9 | 51.2 |
| 7 | MiniCPM-V-2 (2.8B) | LMM 🖼️ | Link | 2024-04-14 | 39.89 | 51.7 | 27.4 | 39.8 | 42.5 | 34.7 | 31.3 | 34.4 | 30.7 | 13.4 | 33.5 | 38.5 | 50.0 |
| 8 | PoT GPT-4 (Caption+OCR) | Tool 🛠️ | Link | 2023-10-03 | 31.74 | 27.6 | 37.4 | 23.9 | 43.0 | 30.3 | 37.1 | 27.9 | 37.5 | 22.7 | 15.8 | 44.5 | 31.9 |
| 9 | CoT GPT4 (Caption+OCR) | Tool 🛠️ | Link | 2023-10-03 | 30.50 | 27.2 | 35.9 | 21.3 | 43.1 | 28.2 | 35.7 | 25.2 | 35.8 | 24.7 | 15.4 | 47.3 | 31.3 |
| 10 | LLaVA (LLaMA-2-13B) | LMM 🖼️ | Link | 2023-10-03 | 25.40 | 22.9 | 24.6 | 18.1 | 35.8 | 29.7 | 26.9 | 22.5 | 24.4 | 19.1 | 19.1 | 34.7 | 21.6 |
| * | Random Chance | - | Link | 2023-10-03 | 17.86 | 15.5 | 24.1 | 4.5 | 23.4 | 24.3 | 25.8 | 13.8 | 22.7 | 13.4 | 8.8 | 15.8 | 14.3 |
🚨 To submit your results to the leaderboard, please send to this email with your result json files.
🚨 For more submission details, please refer to this link and this link.
MathVista Dataset
MathVista is a consolidated Mathematical reasoning benchmark within
Visual contexts. It consists of three newly created datasets, IQTest, FunctionQA, and PaperQA, which address the missing visual domains and are tailored to evaluate logical reasoning on puzzle test figures,
algebraic reasoning over functional plots, and scientific reasoning with academic paper figures, respectively. It also incorporates 9 MathQA datasets
and 19 VQA datasets from the literature, which significantly enrich the diversity and complexity of
visual perception and mathematical reasoning challenges within our benchmark.
In total,
MathVista includes 6,141 examples collected from 31 different datasets.
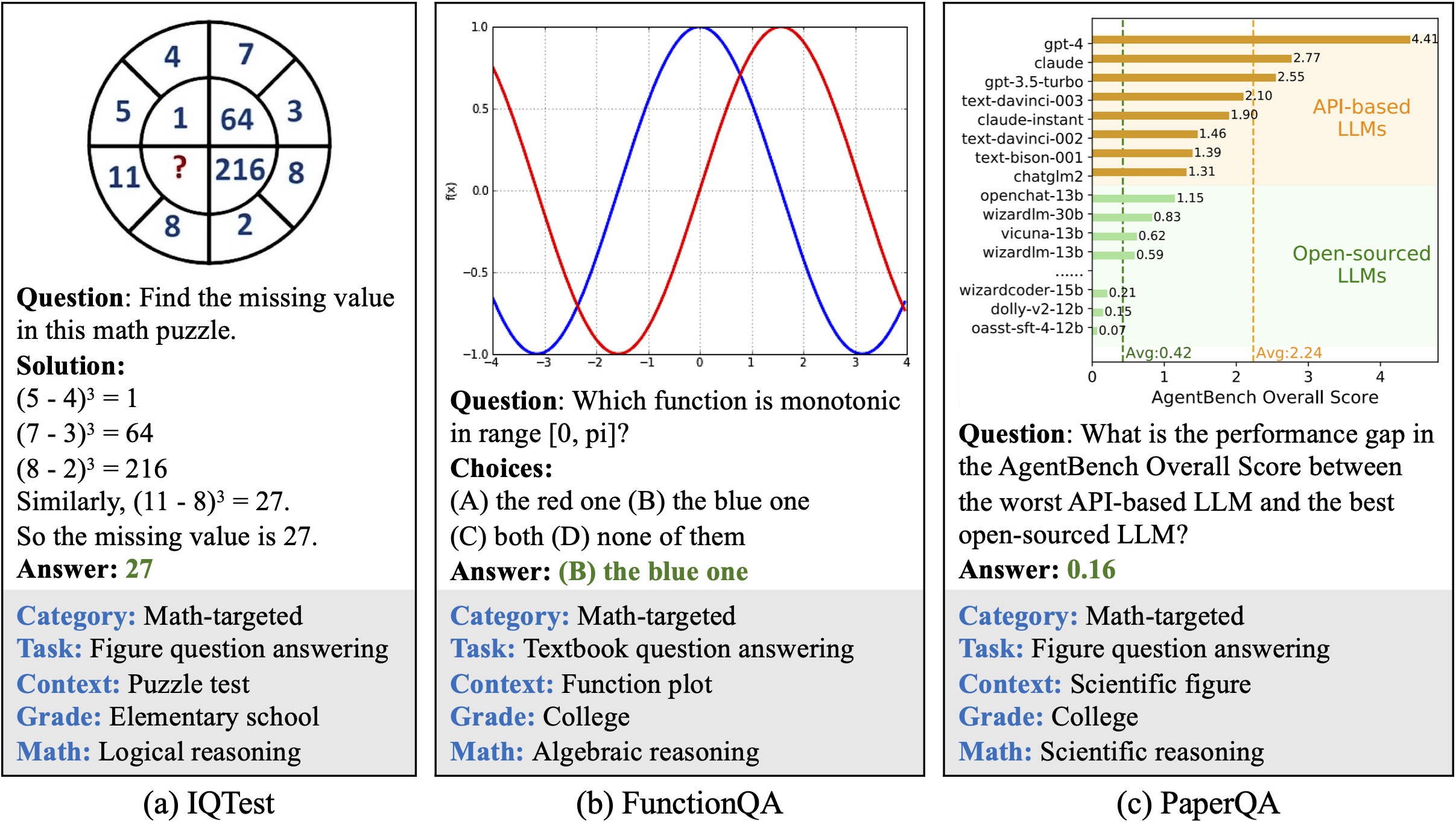
Examples of our newly annotated datasets: IQTest, FunctionQA, and PaperQA.
Summary of the 31 different source datasets in
MathVista.
All the data examples were divided into two subsets: testmini and test.
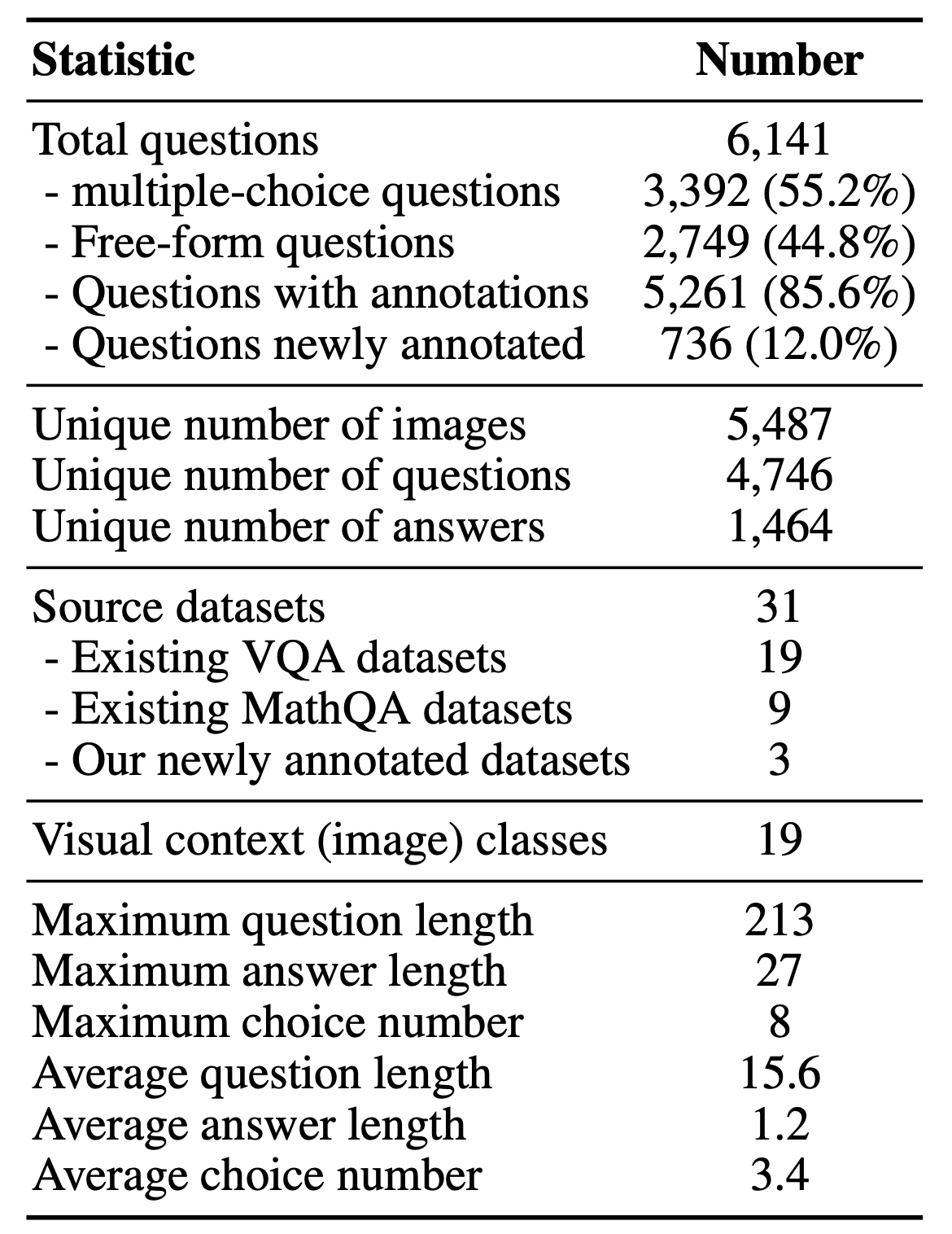
Key statistics of
MathVista.
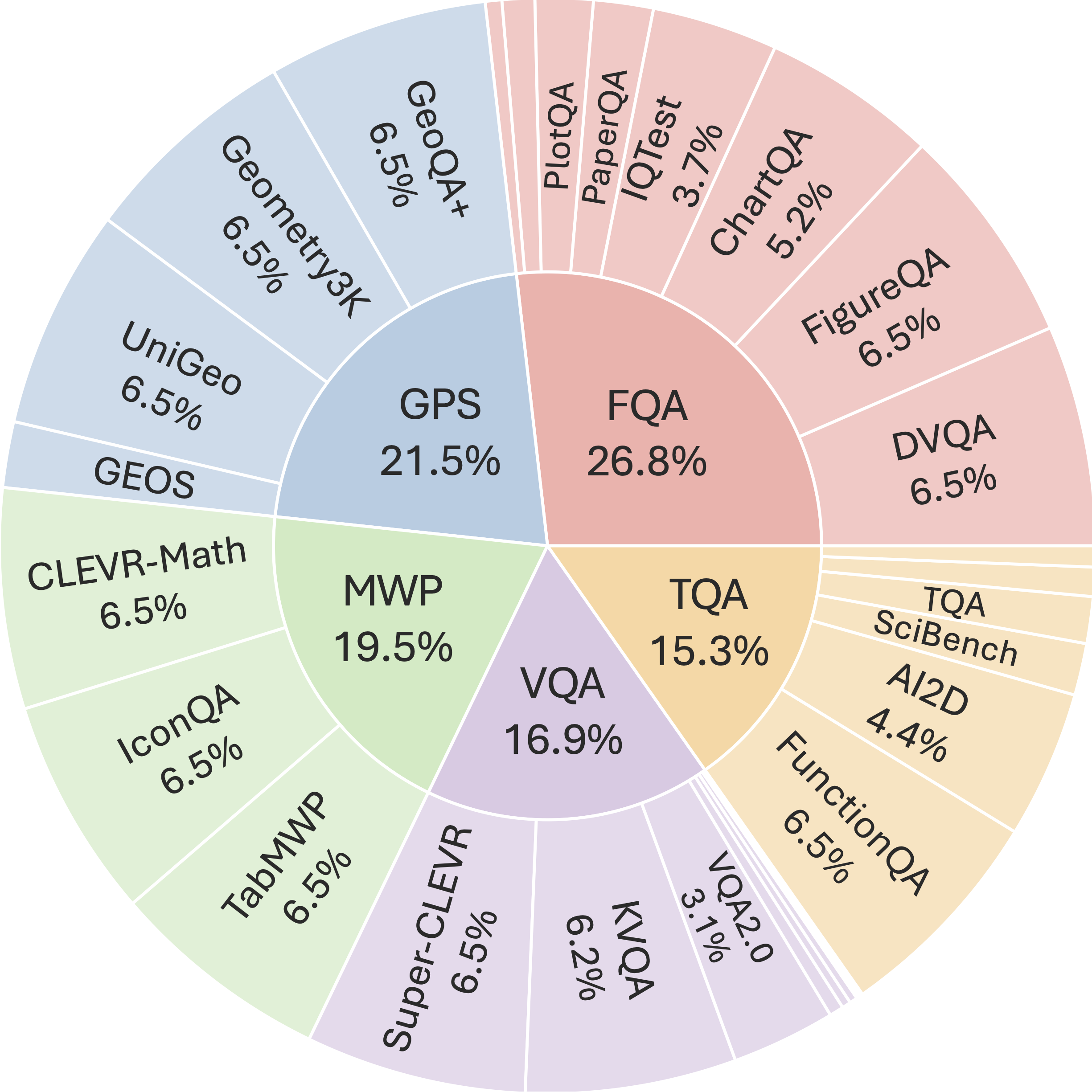
Source dataset distribution of
MathVista.
FQA: figure question answering,
GPS: geometry problem solving,
MWP: math word problem,
TQA: textbook question answering,
VQA: visual question answering.
One example for each mathematical reasoning skill required in
MathVista
Arithmetic Reasoning
Algebraic Reasoning
Geometric Reasoning
Logical Reasoning
Numeric Reasoning
Statistical Reasoning
Scientific Reasoning
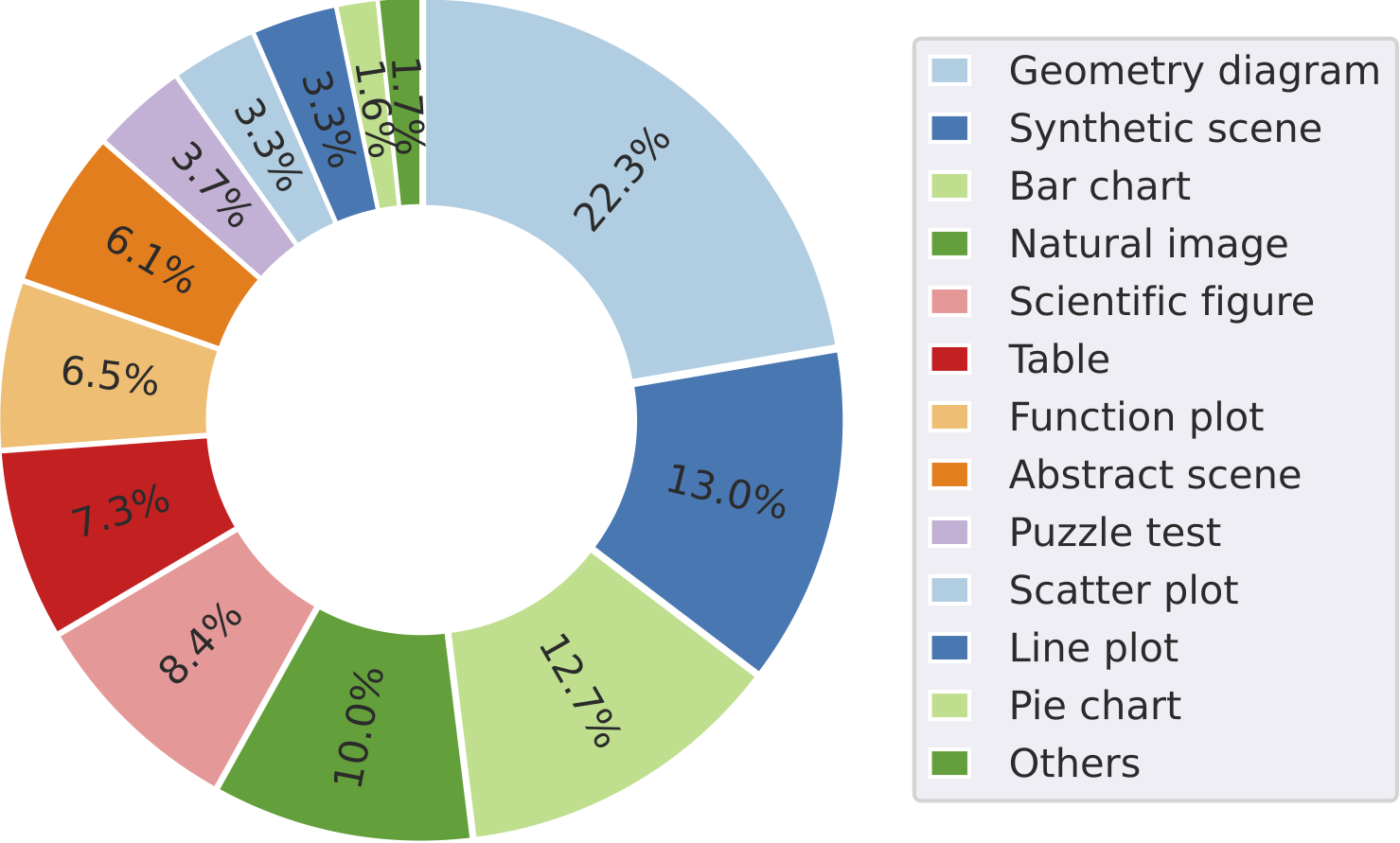
One example for each visual context type required in
MathVista
Geometry Diagram
Synthetic Scene
Bar Chart
Natural Image
Scientific Figure
Table
Function Plot
Abstract Scene
Puzzle Test
Scatter Plot
Line Plot
Pie Chart
Document Image
Medical Image
Others
Notable statistics of
MathVista
Distribution of visual context types within
MathVista
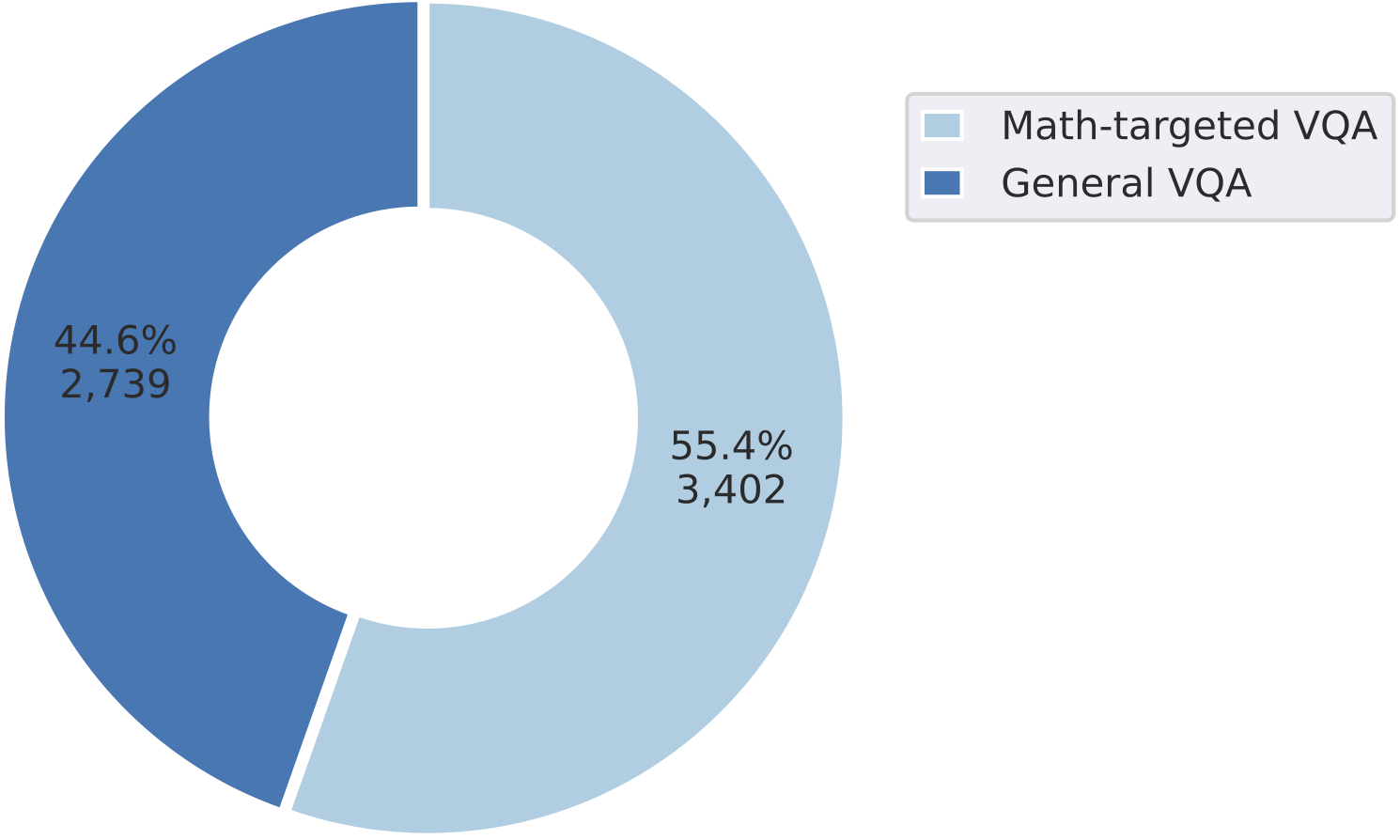
Category distribution of problems within
MathVista
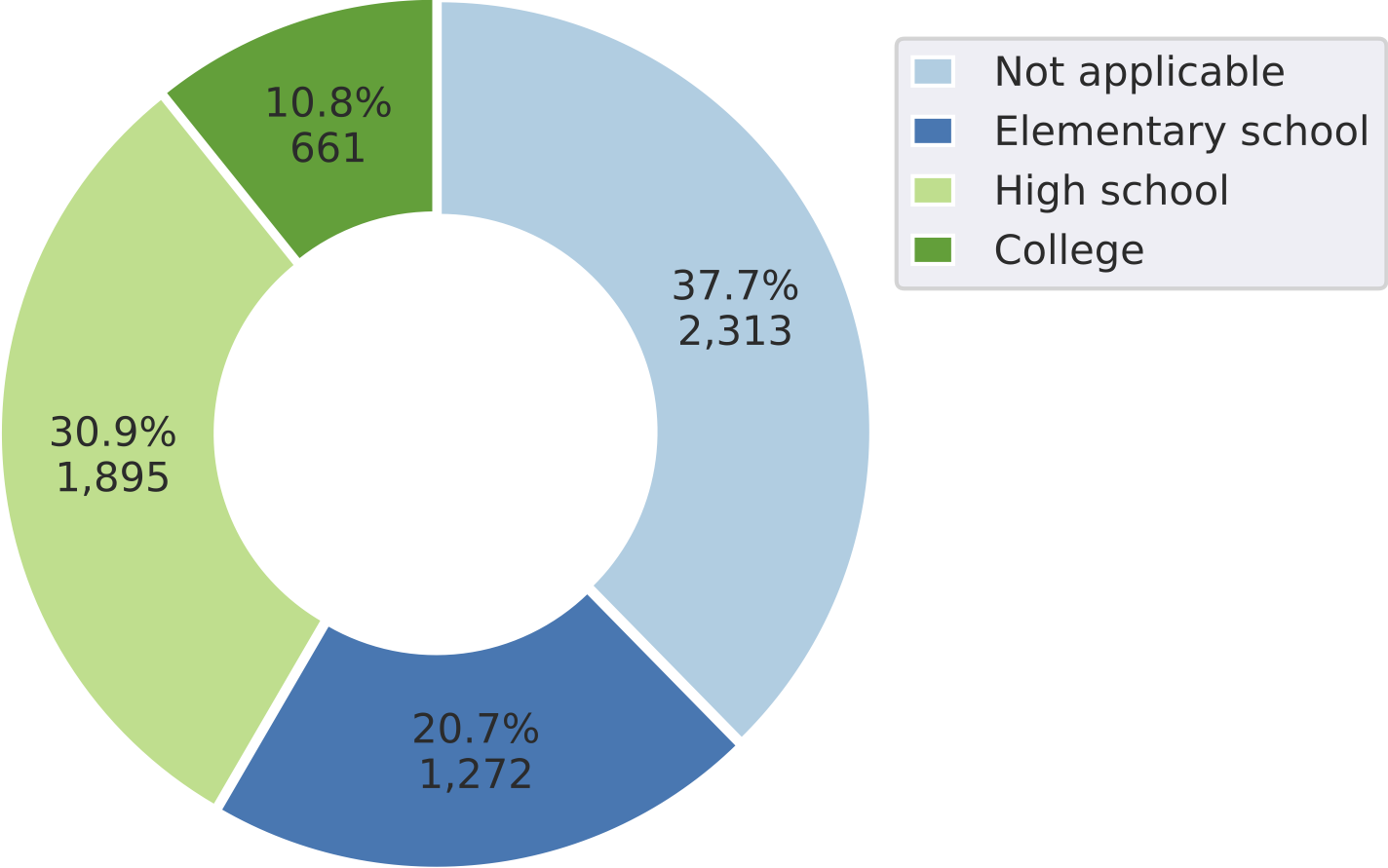
Distribution of questions across different grade levels within
MathVista
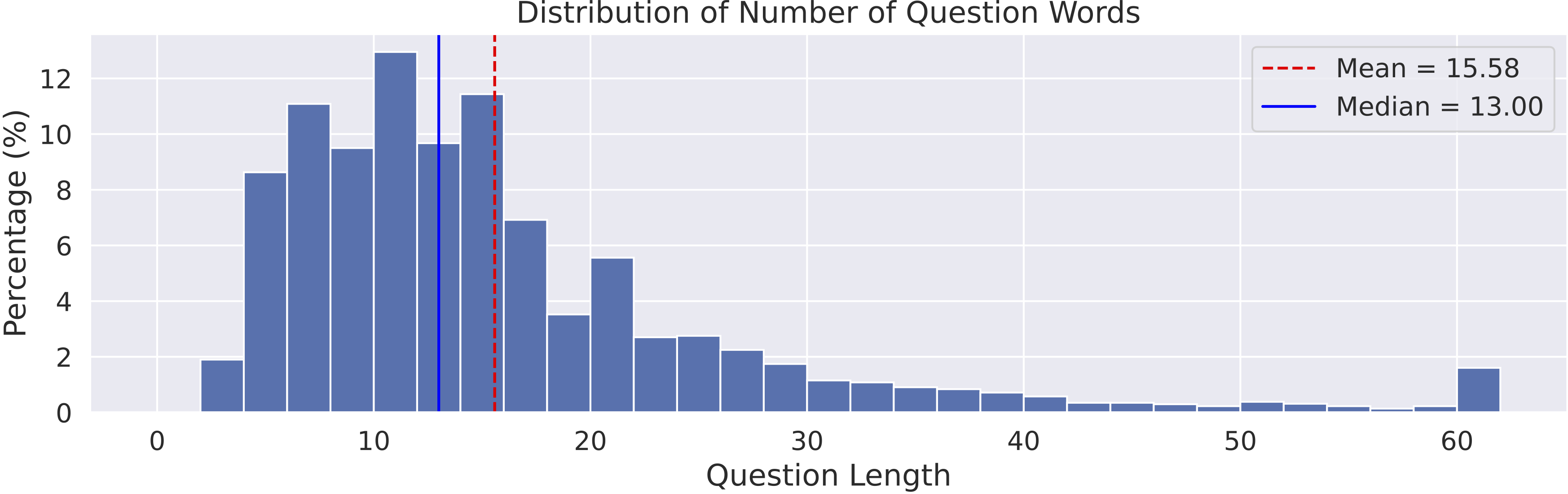
Distribution of the number of words per question in
MathVista.
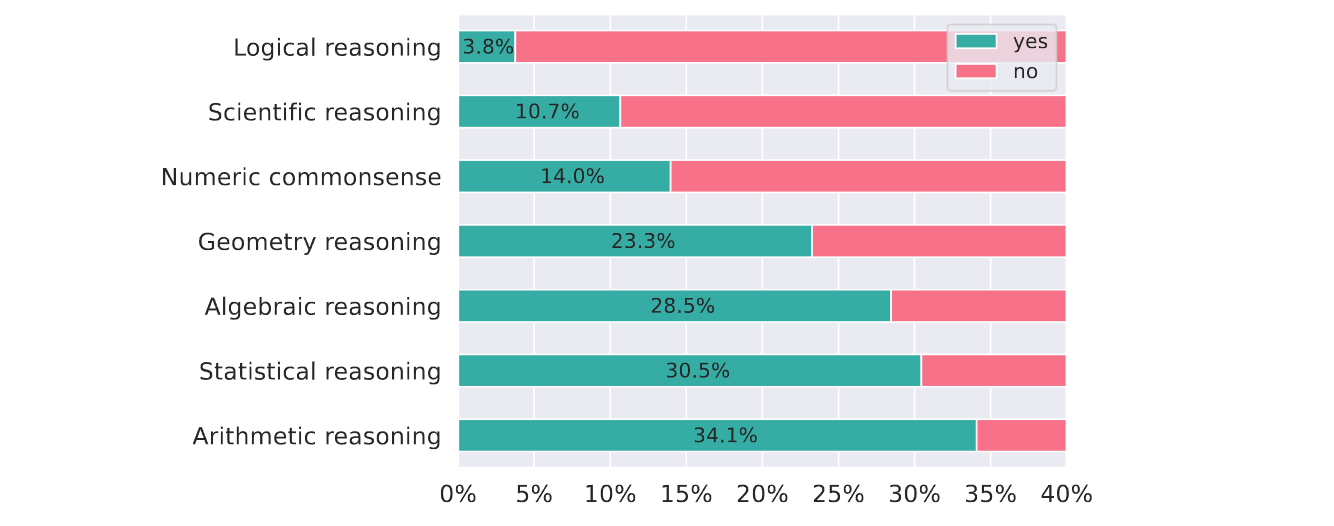
Portion of each mathematical reasoning type involved in the problems of
MathVista
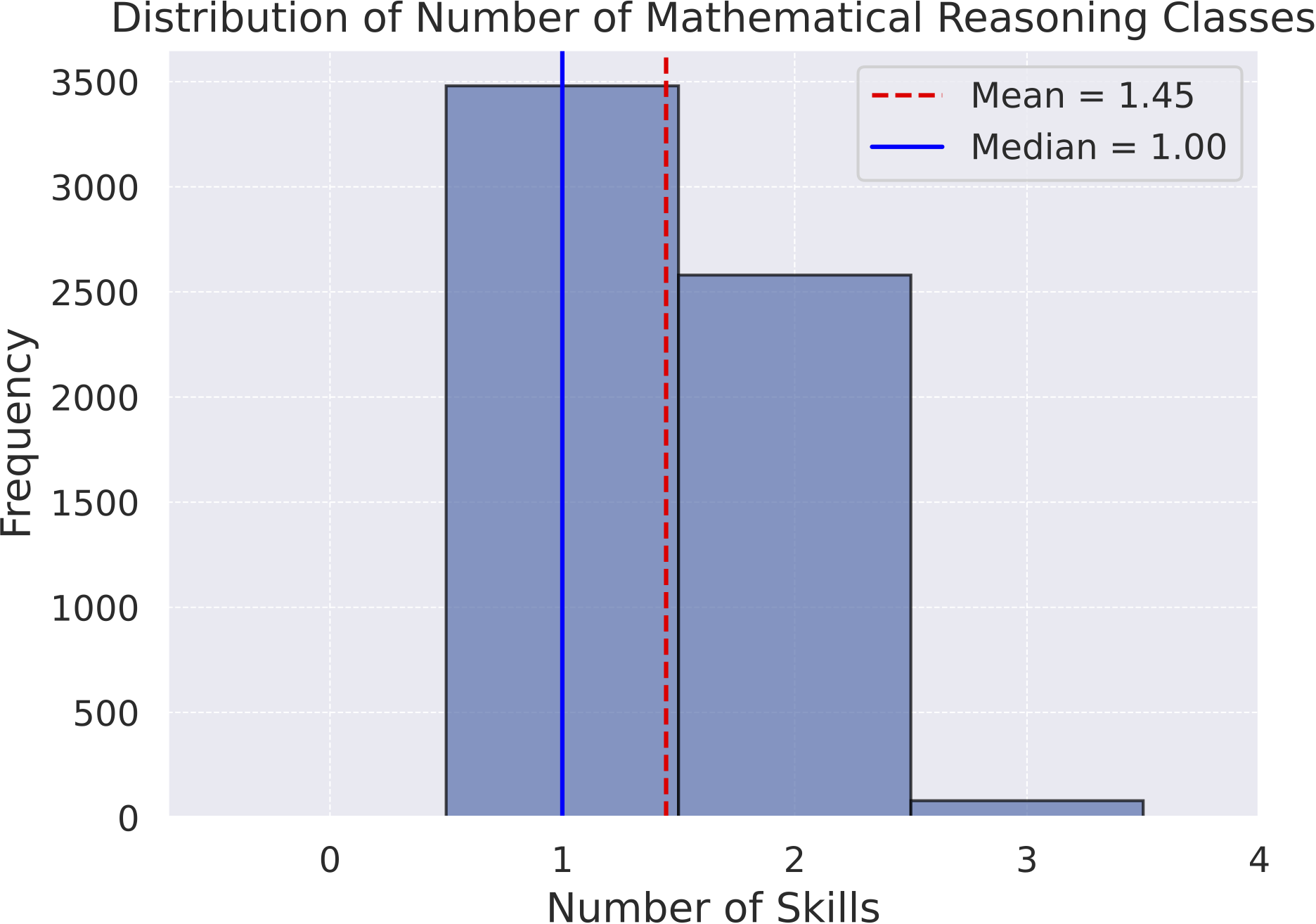
Distribution of the number of mathematical reasoning types within
MathVista
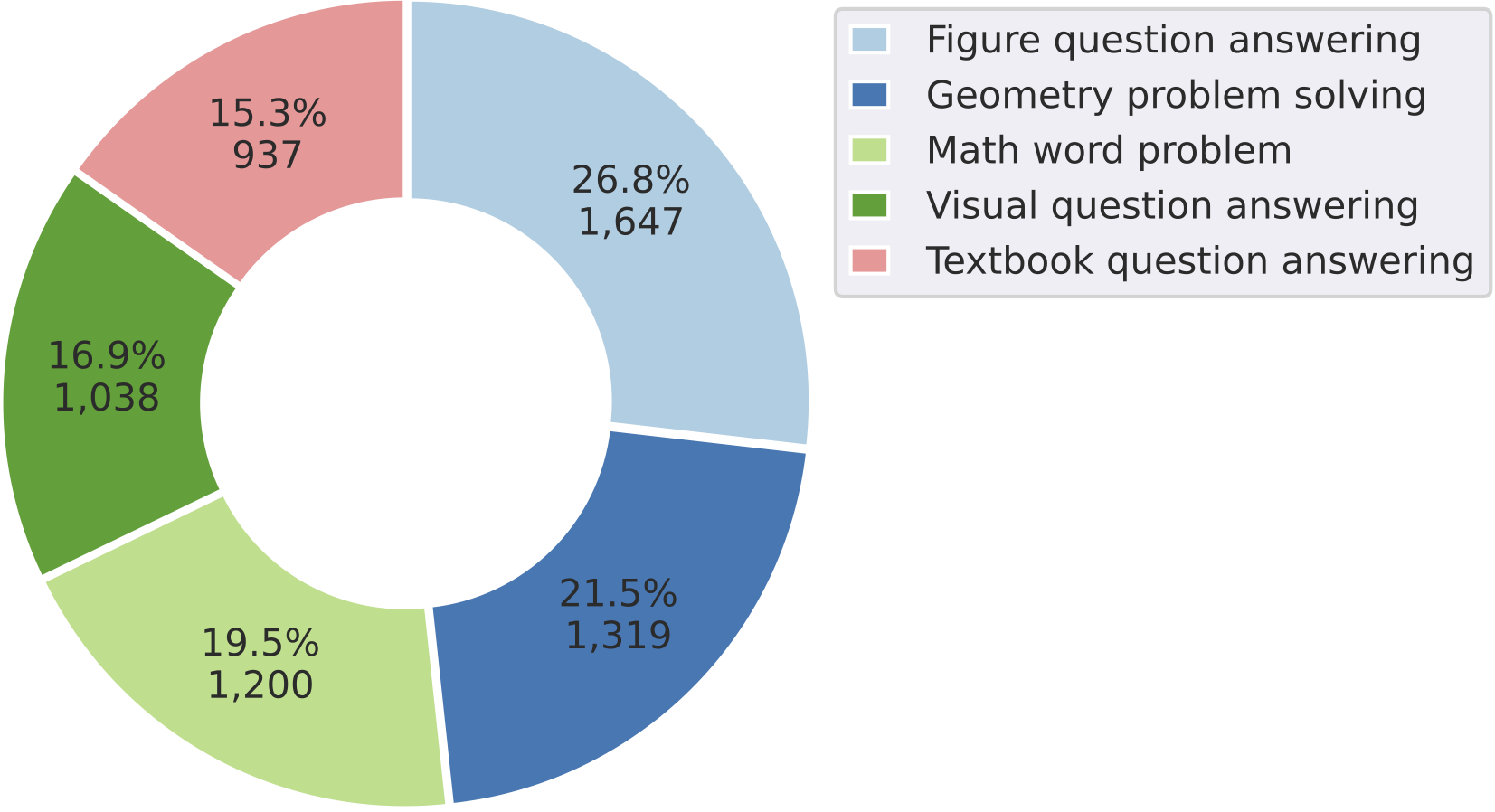
Task type distribution of problems within
MathVista
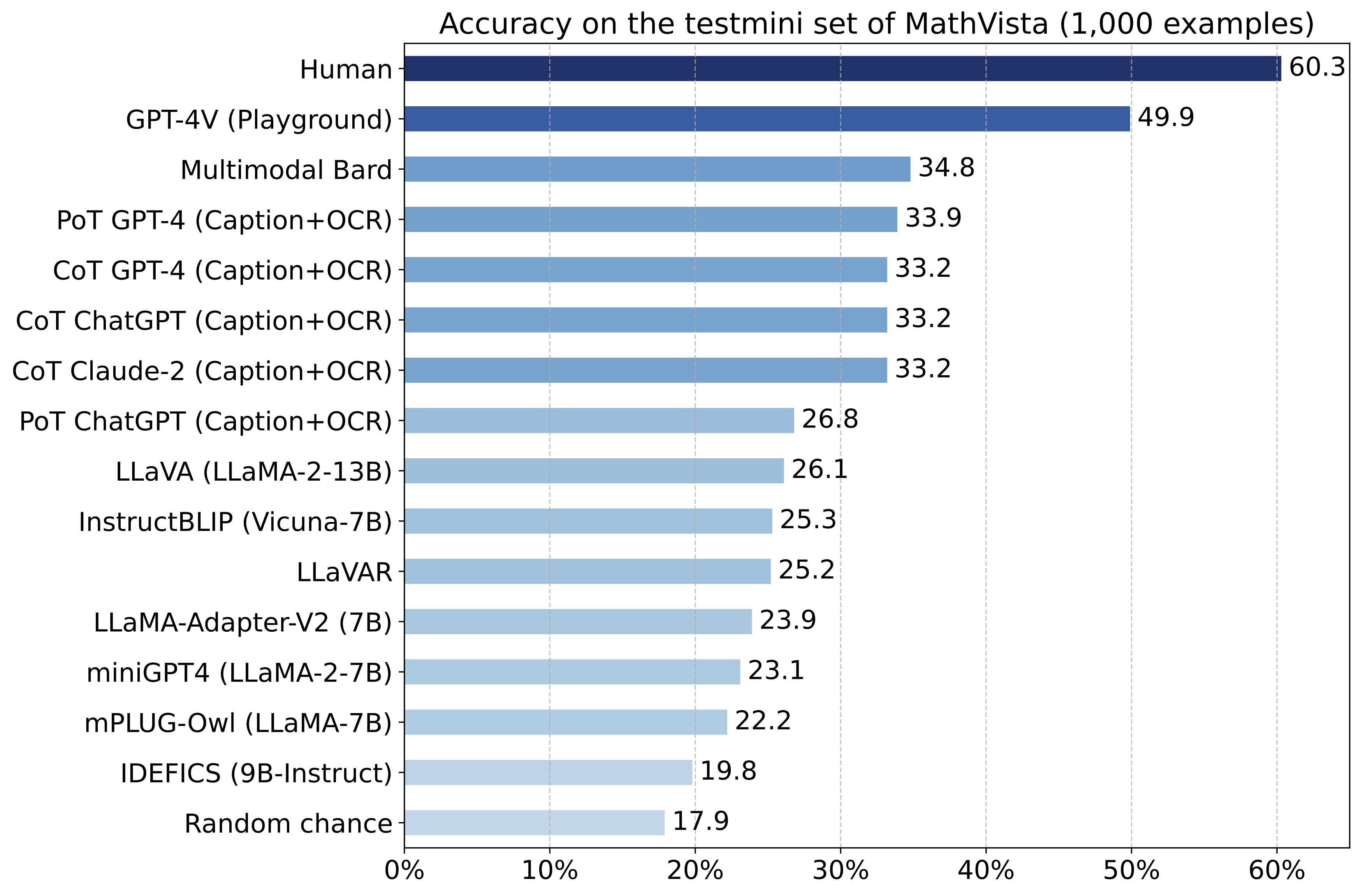
Accuracy scores of primary baselines on the testmini subset (1,000 examples) of
MathVista.
Both CoT GPT-4 and PoT GPT-4 are augmented with Bard captions and OCR text.
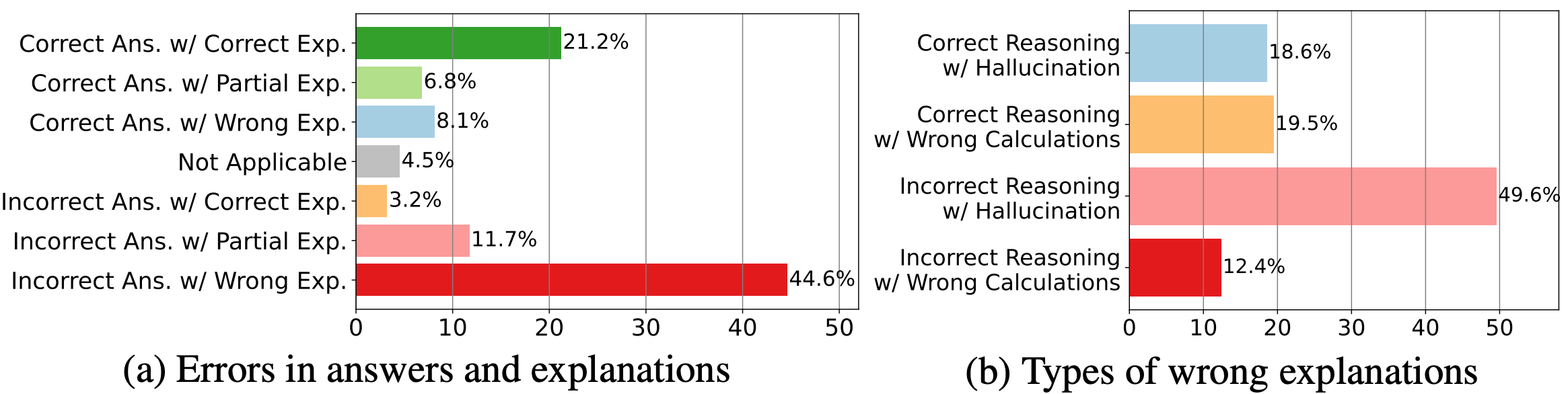
Error analysis of Bard results: (a) presents errors in answers and explanations;
(b) delves into the details of wrong explanations.
Notations: “Answer” is “Ans.”, “Explanation” is “Exp.”, “Partially Correct” is “Partial”,
and “Not applicable” refers to unanswerable or indeterminate cases.
Average accuracy scores across different grade levels for leading foundation models
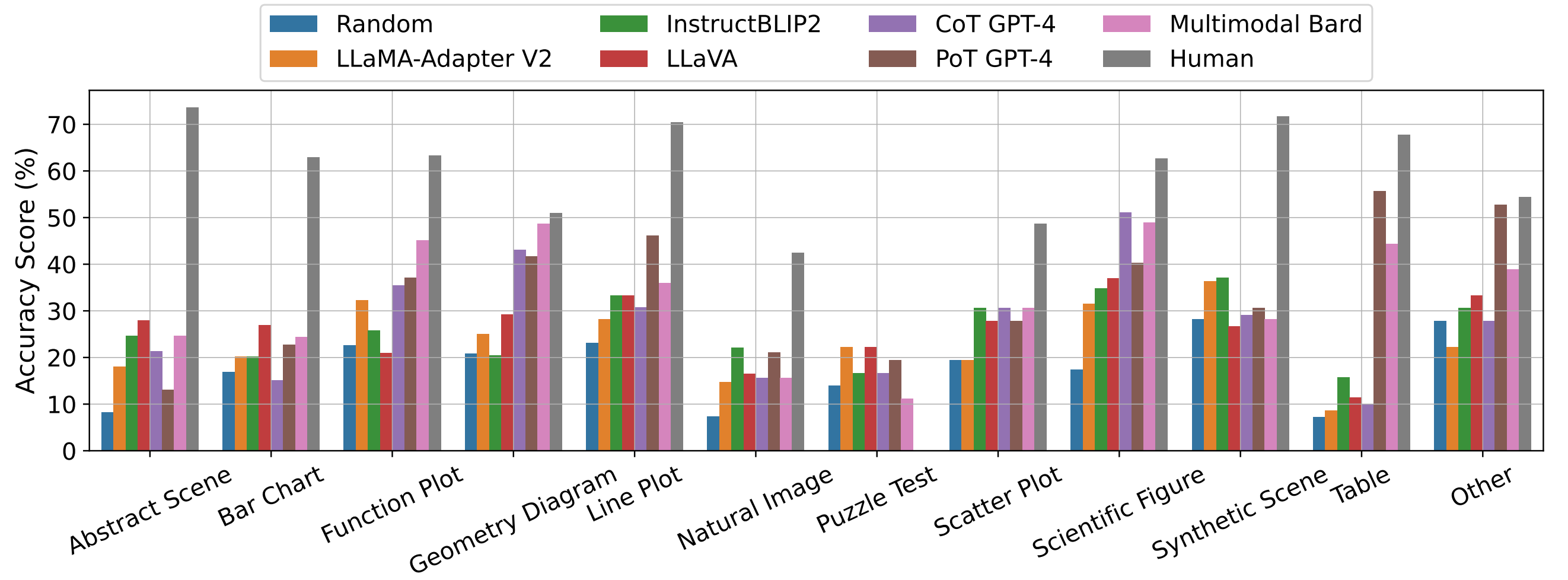
Accuracy scores of leading baselines across various visual contexts
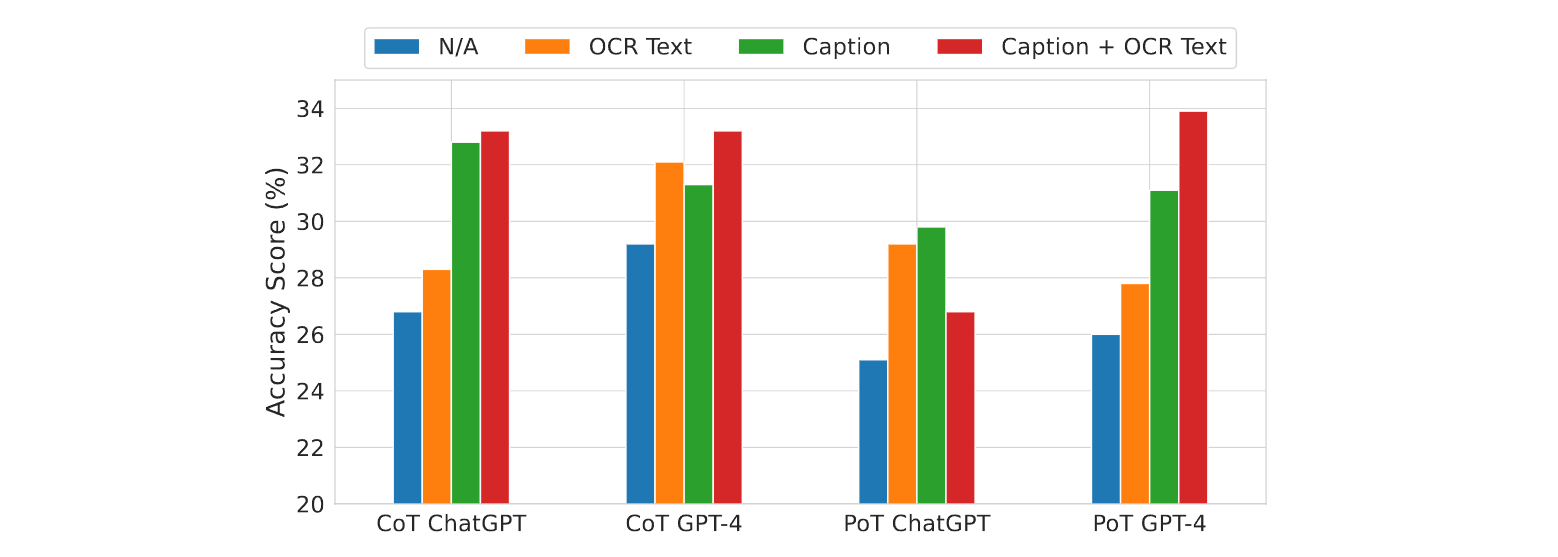
Average accuracy scores of LLM baselines under various visual inputs
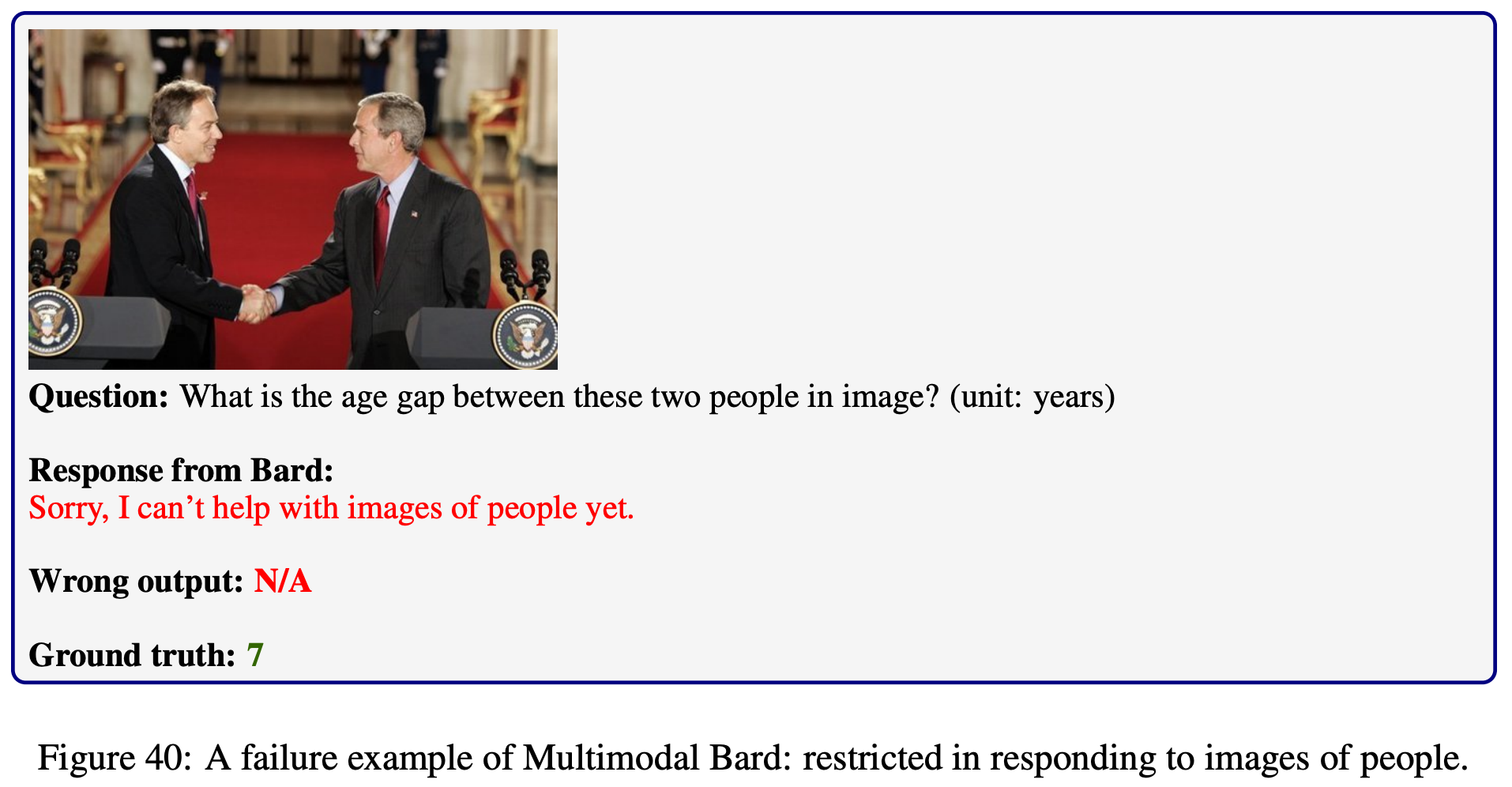
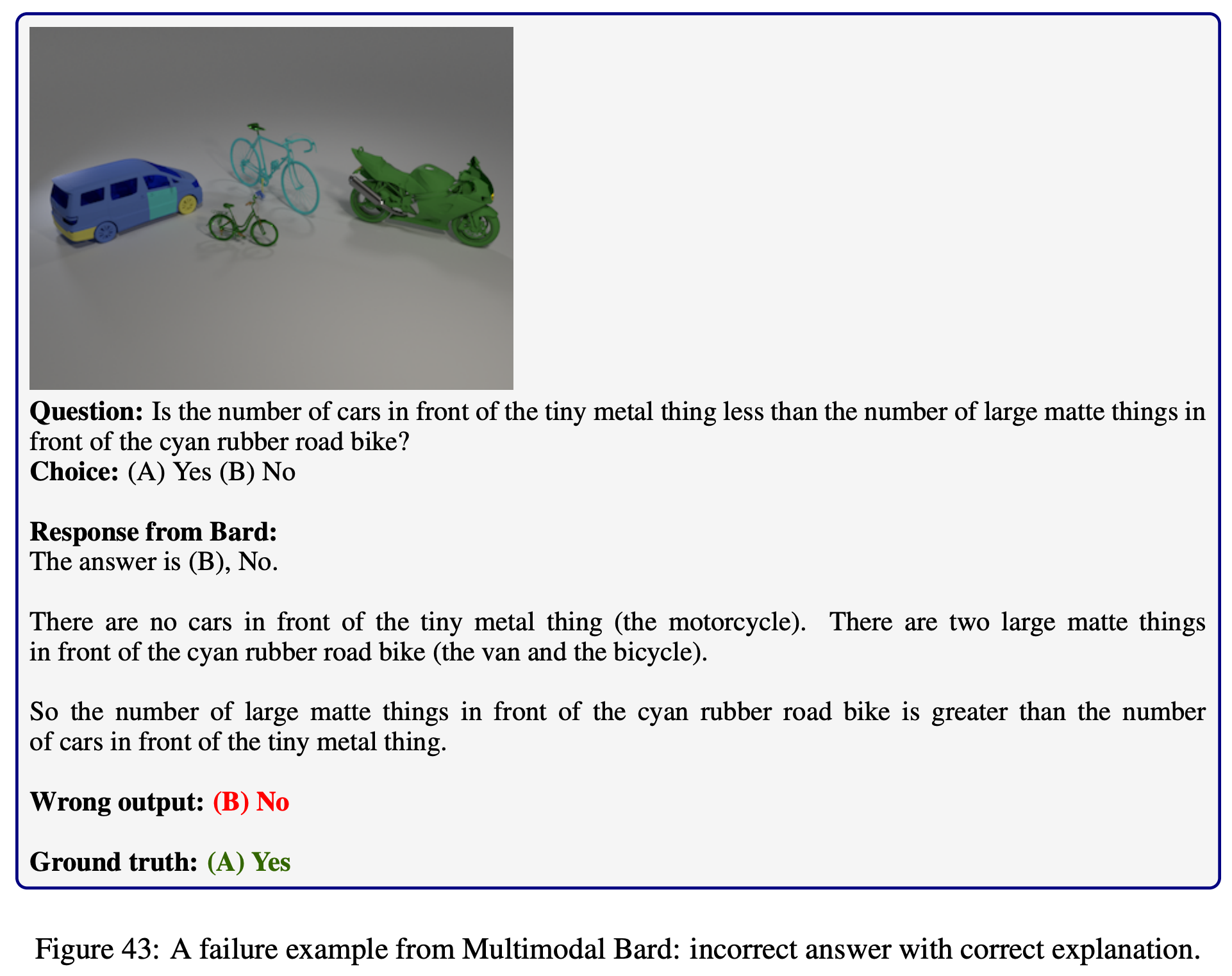
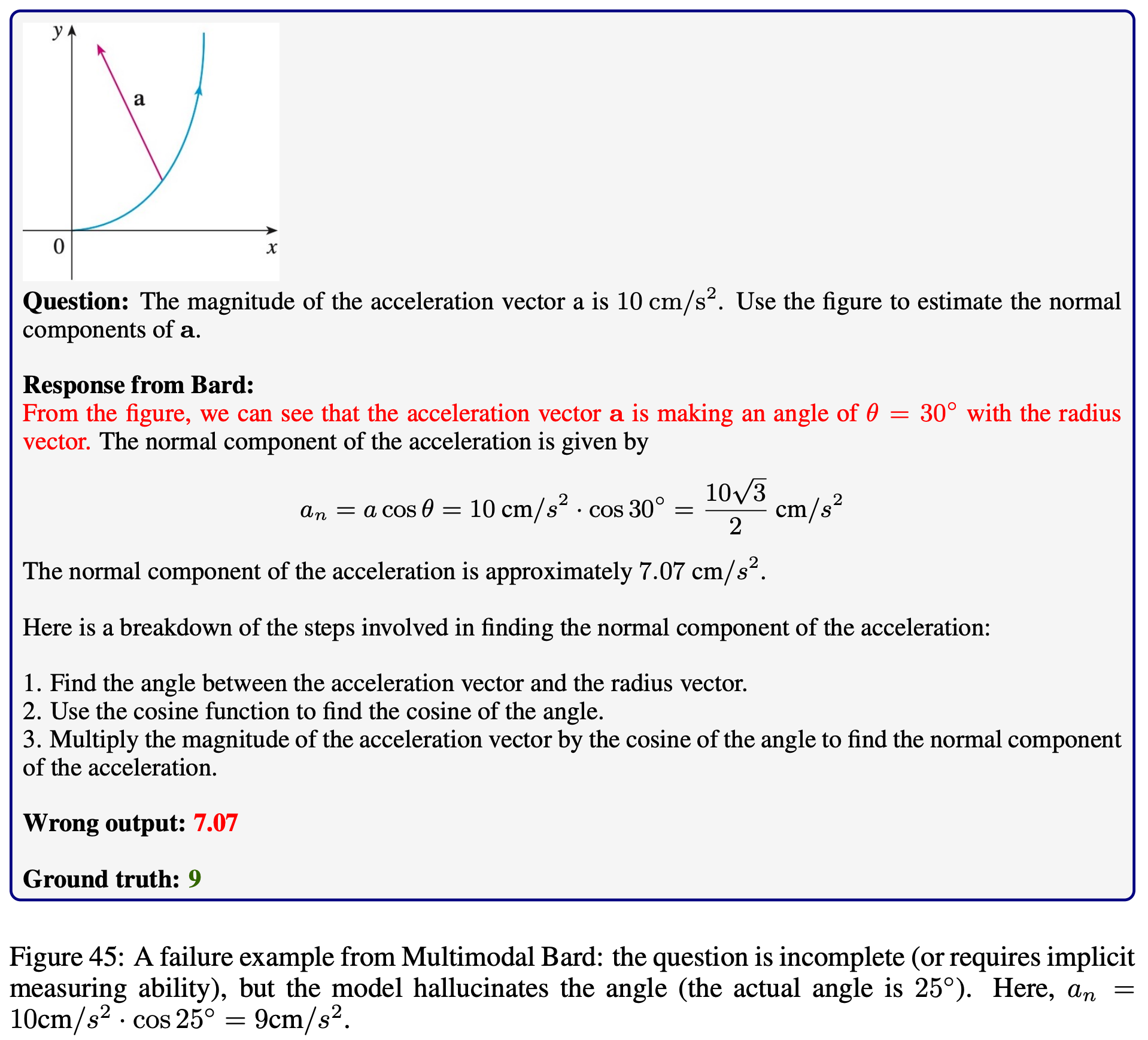
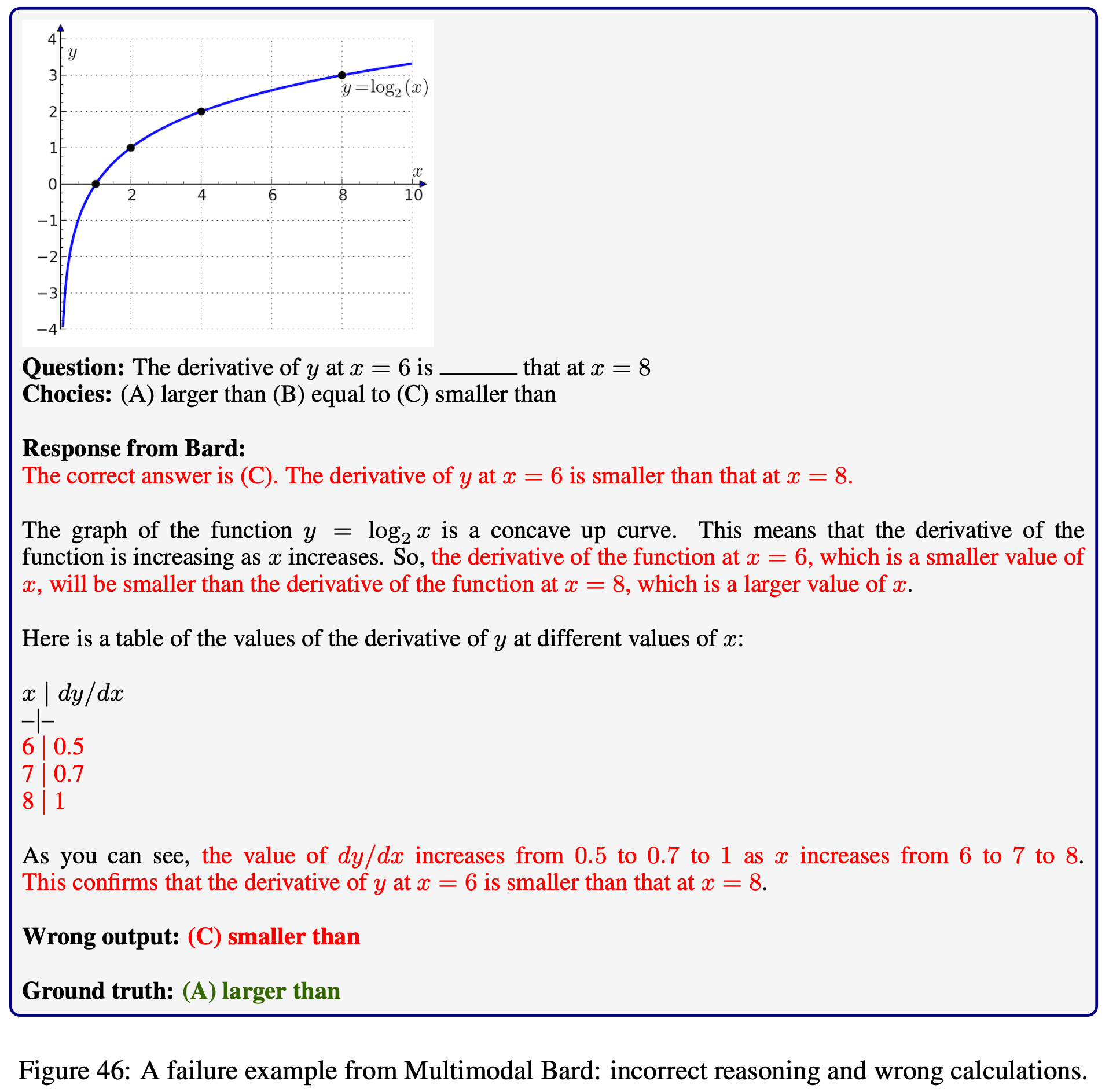
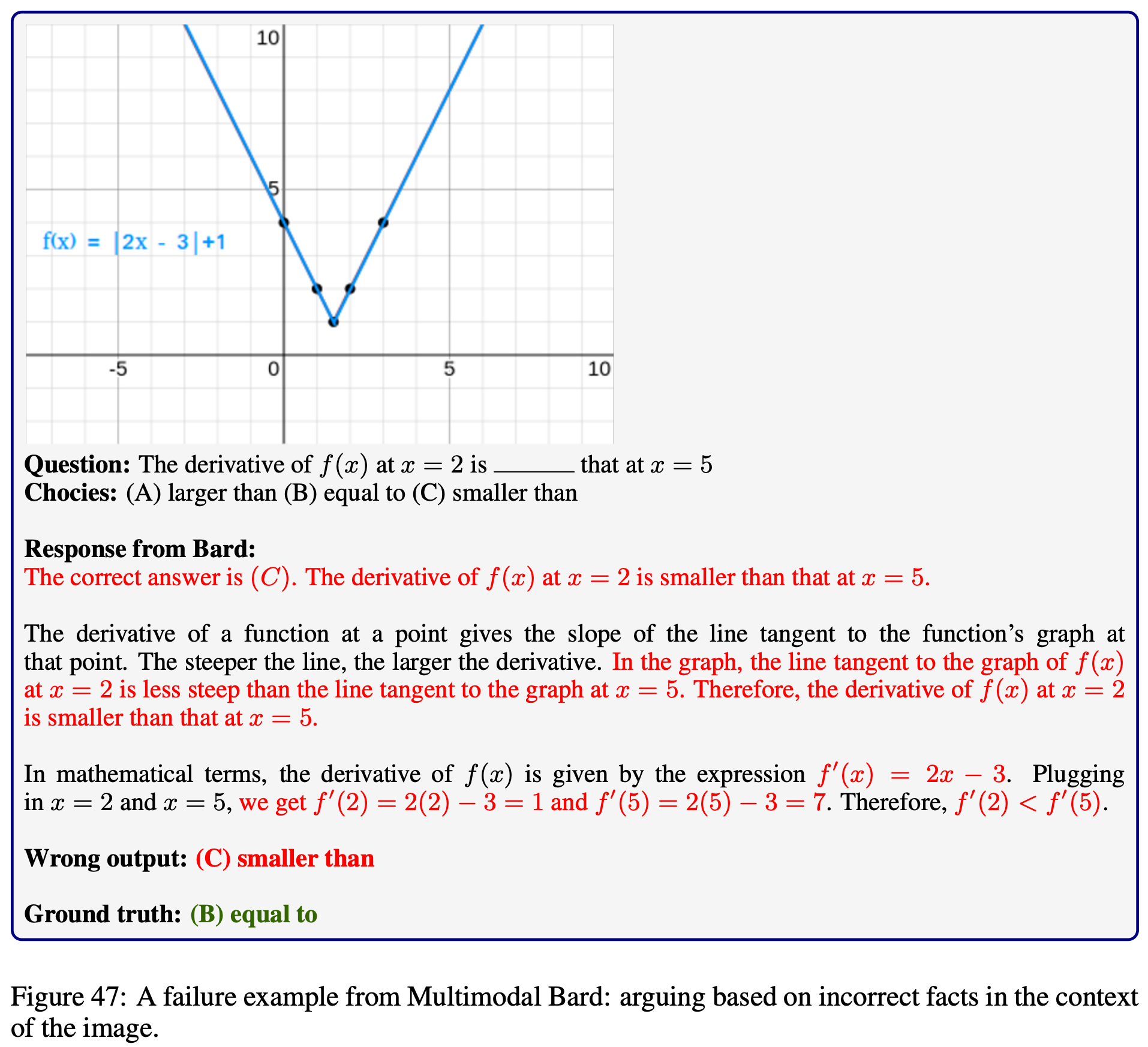
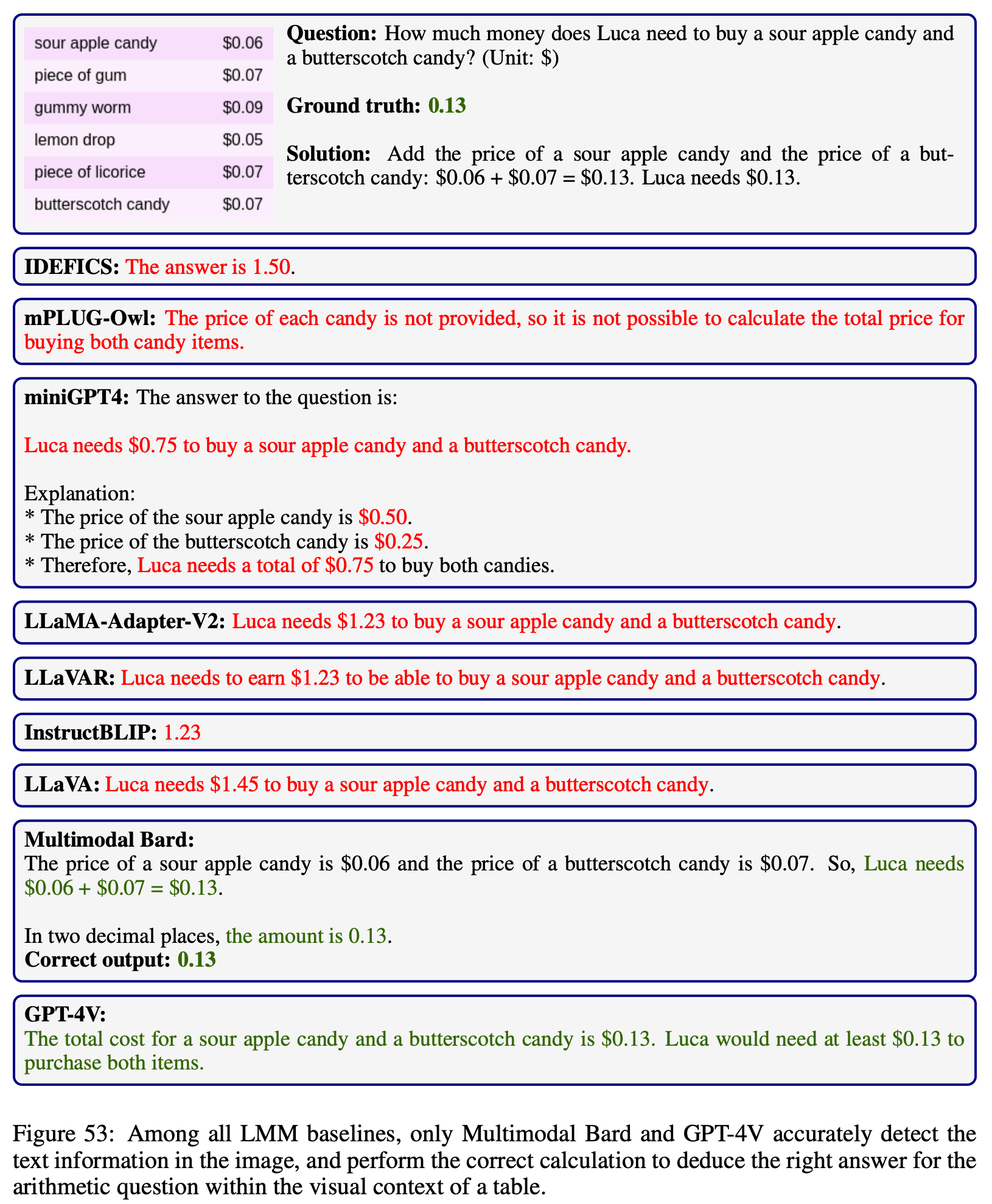
Explore the outputs of each model on
MathVista
@inproceedings{lu2024mathvista,
author = {Lu, Pan and Bansal, Hritik and Xia, Tony and Liu, Jiacheng and Li, Chunyuan and Hajishirzi, Hannaneh and Cheng, Hao and Chang, Kai-Wei and Galley, Michel and Gao, Jianfeng},
title = {MathVista: Evaluating Mathematical Reasoning of Foundation Models in Visual Contexts},
booktitle={International Conference on Learning Representations (ICLR)},
year = {2024}
}
